普里姆算法用于在连通图中寻找最小生成树,该算法的实现采用了贪心的策略。
连通图指的是各个顶点之间至少存在一条通路的无向图。
对于给定的连通图,普里姆算法寻找最小生成树的过程是:
将图中的所有顶点分为 A 类和 B 类,算法执行前,所有顶点都属于 B 类;
从任意顶点出发,同时将此顶点从 B 类划分到 A 类;
从 B 类的所有顶点中,找出到 A 类各个顶点权值最小的一个顶点,将其从 B 类划分到 A 类;
重复执行第 3 步,直至所有顶点全部由 B 类划分到 A 类。
整个过程所历经的路径和顶点,就是一棵最小生成树。
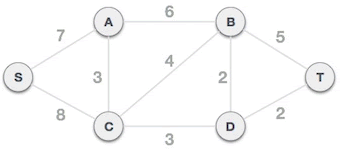
图 1 图存储结构
我们以图 1 所示的连通图为例,如下为普里姆算法寻找最小生成树的过程:
1) 将所有顶点分为两类,类 A={},类 B={A,B,C,D,S,T};
2) 假设从 S 顶点出发寻找最小生成树,则 A={S},B={A,B,C,D,T}。从图 1 可以看出,B 类的所有顶点到顶点 S 权值最小的路径为 (S,A),所以我们选择 (S,A) 组成最小生成树(如图 2 所示),同时将顶点 A 划分到 A 类。
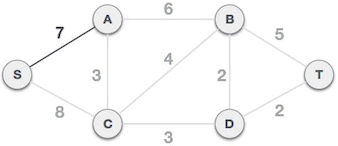
图 2 寻找最小生成树_过程 1
3) 此时 A={S,A},B={B,C,D,T},B 类顶点和 A 类顶点之间的路径有 (S,C)、(A,C)、(A,B),权值最小的路径为 (A,C),所以我们选择 (A,C) 组成最小生成树(如图 3 所示),同时将顶点 C 划分到 A 类。
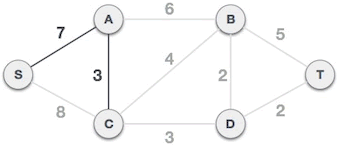
图 3 寻找最小生成树_过程 2
4) 此时 A={S,A,C},B={B,D,T},B 类顶点和 A 类顶点之间的路径有 (S,C)、(A,B)、(C,B)、(C,D),权值最小的路径为 (C,D),所以我们选择 (C,D) 组成最小生成树(如图 4 所示),同时将顶点 D 划分到 A 类。
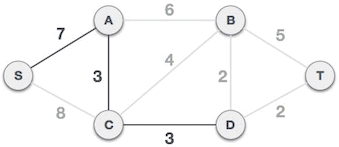
图 4 寻找最小生成树_过程 3
5) 此时 A={S,A,C,D},B={B,T},B 类顶点和 A 类顶点之间的路径有 (S,C)、(A,B)、(C,B)、(D,B)、(D,T),权值最小的路径有 2 个,分别是 (B,D) 和 (T,D)。任选其中的一个,比如选择 (B,D),将顶点 B 划分到 A 类。
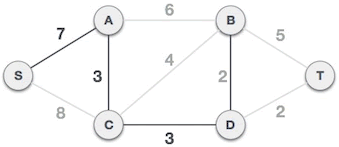
图 5 寻找最小生成树_过程 4
6) 此时 A={S,A,C,D,B},B={T},B 类顶点 T 和 A 类顶点之间的路径有 (B,T)、(D,T),权值最小的路径为 (D,T),因此选择 (D,T) 组成最小生成树(如图 6 所示),同时将顶点 T 划分到 A 类。
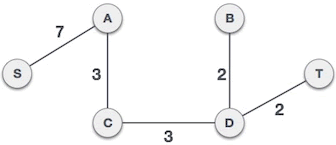
图 6 寻找最小生成树_过程 5
7) 此时 A={S,A,C,D,B,T},B={},A 类已经包含了图中的所有顶点,查找结束,图 6 即为普里姆算法寻找的最小生成树。
如下为普里姆算法寻找最小生成树的伪代码:
V // 输入图中顶点的总个数
cost[V][V] // 输入图中顶点之间路径的权值
find_MST(cost[V][V]):
parent[V] // 记录最小生成树中各个顶点的父节点的位置
key[V] // 统计未选中的顶点(类B)到已选中的顶点(类A)之间的权值(存储最小的一个)
visited[V] // 记录各个顶点属于类 A 还是类 B
for i<-0 to V:
key[i] <- INF // 将 key 中的各个位置初始化为无限大的值
visited[i] <- false // 初始阶段,所有顶点都位于类 B 中
parent[i] <- -1 // 初始阶段,还没有最小生成树,各个顶点没有父节点
key[0] <- 0 // 从位置为 0 处的顶点出发,寻找最小生成书
parent[0] <- -1 // 位置为 0 的顶点没有父节点
for i <- 0 to V-1: // 最小生成树中的路径总数为顶点数-1
u = min_key(key,visited) // 查找 key 数组中记录的权值最小的顶点所在的下标
visited[u] = true // 将下标为 u 的顶点划分为 A 类中
for v <- 0 to V: // 更新 key 数组中各个 B 类顶点到 A 类顶点的权值
// 如果该顶点属于 B 类,且权值小于当前记录的权值
if visited[V] == false && cost[u][v] < key[v]:
// 更新父节点的信息,同时更新 key 数组记录的权值
parent[v] <- u;
key[v] <- cost[u][v]
return parent // 根据 parent 记录的各个顶点的父节点信息,可以输出最小生成树各个顶点以及相关路径的信息
普里姆算法的具体实现
结合伪代码,如下为普里姆算法寻找最小生成树的 C 语言程序:
#include<stdio.h>
#define V 6 // 记录图中顶点的个数
typedef enum { false, true } bool;
//查找权值最小的、尚未被选择的顶点,key 数组记录了各顶点之间的权值数据,visited数组记录着各个顶点是否已经被选择的信息
int min_Key(int key[], bool visited[])
{
int min = 2147483647, min_index; //遍历 key 数组使用,min 记录最小的权值,min_index 记录最小权值关联的顶点
//遍历 key 数组
for (int v = 0; v < V; v++) {
//如果当前顶点为被选择,且对应的权值小于 min 值
if (visited[v] == false && key[v] < min) {
//更新 min 的值并记录该顶点的位置
min = key[v];
min_index = v;
}
}
//返回最小权值的顶点的位置
return min_index;
}
//输出最小生成树
void print_MST(int parent[], int cost[V][V])
{
int minCost = 0;
printf("最小生成树为:\n");
//遍历 parent 数组
for (int i = 1; i < V; i++) {
//parent 数组下标值表示各个顶点,各个下标对应的值为该顶点的父节点
printf("%d - %d wight:%d\n", parent[i]+1, i+1, cost[i][parent[i]]);//由于数组下标从 0 开始,因此输出时各自 +1
//统计最小生成树的总权值
minCost += cost[i][parent[i]];
}
printf("总权值为:%d", minCost);
}
//根据用户提供了图的信息(存储在 cost 数组中),寻找最小生成树
void find_MST(int cost[V][V])
{ //key 数组用于记录 B 类顶点到 A 类顶点的权值
//parent 数组用于记录最小生成树中各个顶点父节点的位置,便于最终生成最小生成树
//visited 数组用于记录各个顶点属于 A 类还是 B 类
int parent[V], key[V];
bool visited[V];
// 初始化 3 个数组
for (int i = 0; i < V; i++) {
key[i] = 2147483647; // 将 key 数组各个位置设置为无限大的数
visited[i] = false; // 所有的顶点全部属于 B 类
parent[i] = -1; // 所有顶点都没有父节点
}
// 选择 key 数组中第一个顶点,开始寻找最小生成树
key[0] = 0; // 该顶点对应的权值设为 0
parent[0] = -1; // 该顶点没有父节点
// 对于 V 个顶点的图,最需选择 V-1 条路径,即可构成最小生成树
for (int x = 0; x < V - 1; x++)
{
// 从 key 数组中找到权值最小的顶点所在的位置
int u = min_Key(key, visited);
// 该顶点划分到 A 类
visited[u] = true;
// 由于新顶点加入 A 类,因此需要更新 key 数组中的数据
for (int v = 0; v < V; v++)
{
// 如果类 B 中存在到下标为 u 的顶点的权值比 key 数组中记录的权值还小,表明新顶点的加入,使得类 B 到类 A 顶点的权值有了更好的选择
if (cost[u][v] != 0 && visited[v] == false && cost[u][v] < key[v])
{
// 更新 parent 数组记录的各个顶点父节点的信息
parent[v] = u;
// 更新 key 数组
key[v] = cost[u][v];
}
}
}
//根据 parent 记录的各个顶点父节点的信息,输出寻找到的最小生成树
print_MST(parent, cost);
}
// main function
int main()
{
int p1, p2;
int wight;
int cost[V][V] = { 0 };
printf("输入图(顶点到顶点的路径和权值:)\n");
while (1) {
scanf("%d %d", &p1, &p2);
//如果用户输入 -1 -1,表示输入结束
if (p1 == -1 && p2 == -1) {
break;
}
scanf("%d", &wight);
cost[p1-1][p2-1] = wight;
cost[p2-1][p1-1] = wight;
}
// 根据用户输入的图的信息,寻找最小生成树
find_MST(cost);
return 0;
}
如下为普里姆算法寻找最小生成树的 Java 程序:
import java.util.Scanner;
public class prim {
static int V = 6;
public static int min_Key(int []key,boolean []visited) {
//遍历 key 数组使用,min 记录最小的权值,min_index 记录最小权值关联的顶点
int min = 2147483647,min_index = 0;
//遍历 key 数组
for (int v = 0; v < V; v++) {
//如果当前顶点为被选择,且对应的权值小于 min 值
if (visited[v] == false && key[v] < min) {
//更新 min 的值并记录该顶点的位置
min = key[v];
min_index = v;
}
}
//返回最小权值的顶点的位置
return min_index;
}
public static void print_MST(int []parent, int [][]cost) {
int minCost = 0;
System.out.println("最小生成树为:");
//遍历 parent 数组
for (int i = 1; i < V; i++) {
//parent 数组下标值表示各个顶点,各个下标对应的值为该顶点的父节点
System.out.println((parent[i]+1)+" - "+(i+1)+" wight:"+cost[i][parent[i]]);//由于数组下标从 0 开始,因此输出时各自 +1
//统计最小生成树的总权值
minCost += cost[i][parent[i]];
}
System.out.print("总权值为:"+minCost);
}
public static void find_MST(int [][]cost) {
//key 数组用于记录 B 类顶点到 A 类顶点的权值
//parent 数组用于记录最小生成树中各个顶点父节点的位置,便于最终生成最小生成树
//visited 数组用于记录各个顶点属于 A 类还是 B 类
int []parent = new int[V];
int []key = new int[V];
boolean []visited=new boolean[V];
// 初始化 3 个数组
for (int i = 0; i < V; i++) {
key[i] = 2147483647; // 将 key 数组各个位置设置为无限大的数
visited[i] = false; // 所有的顶点全部属于 B 类
parent[i] = -1; // 所有顶点都没有父节点
}
// 选择 key 数组中第一个顶点,开始寻找最小生成树
key[0] = 0; // 该顶点对应的权值设为 0
parent[0] = -1; // 该顶点没有父节点
// 对于 V 个顶点的图,最需选择 V-1 条路径,即可构成最小生成树
for (int x = 0; x < V - 1; x++)
{
// 从 key 数组中找到权值最小的顶点所在的位置
int u = min_Key(key, visited);
// 该顶点划分到 A 类
visited[u] = true;
// 由于新顶点加入 A 类,因此需要更新 key 数组中的数据
for (int v = 0; v < V; v++)
{
// 如果类 B 中存在到下标为 u 的顶点的权值比 key 数组中记录的权值还小,表明新顶点的加入,使得类 B 到类 A 顶点的权值有了更好的选择
if (cost[u][v] != 0 && visited[v] == false && cost[u][v] < key[v])
{
// 更新 parent 数组记录的各个顶点父节点的信息
parent[v] = u;
// 更新 key 数组
key[v] = cost[u][v];
}
}
}
//根据 parent 记录的各个顶点父节点的信息,输出寻找到的最小生成树
print_MST(parent, cost);
}
public static void main(String[] args) {
int [][]cost = new int[V][V];
System.out.println("输入图(顶点到顶点的路径和权值:)");
Scanner sc = new Scanner(System.in);
while (true) {
int p1 = sc.nextInt();
int p2 = sc.nextInt();
// System.out.println(p1+p2);
if (p1 == -1 && p2 == -1) {
break;
}
int wight = sc.nextInt();
cost[p1-1][p2-1] = wight;
cost[p2-1][p1-1] = wight;
}
// 根据用户输入的图的信息,寻找最小生成树
find_MST(cost);
}
}
如下为普里姆算法寻找最小生成树的 Python 程序:
V = 6 #图中顶点的个数
cost = [[0]*V for i in range(V)]
print("输入图(顶点到顶点的路径和权值:)")
while True:
li = input().split()
p1 = int(li[0])
p2 = int(li[1])
if p1 == -1 and p2 == -1:
break
wight = int(li[2])
cost[p1-1][p2-1] = wight
cost[p2-1][p1-1] = wight
#查找权值最小的、尚未被选择的顶点,key 列表记录了各顶点之间的权值数据,visited列表记录着各个顶点是否已经被选择的信息
def min_Key(key,visited):
#遍历 key 列表使用,min 记录最小的权值,min_index 记录最小权值关联的顶点
min = float('inf')
min_index = 0
#遍历 key 列表
for v in range(V):
#如果当前顶点为被选择,且对应的权值小于 min 值
if visited[v] == False and key[v]<min:
#更新 min 的值并记录该顶点的位置
min = key[v]
min_index=v
#返回最小权值的顶点的位置
return min_index
#输出最小生成树
def print_MST(parent,cost):
minCost=0
print("最小生成树为:")
#遍历 parent 列表
for i in range(1,V):
#parent 列表下标值表示各个顶点,各个下标对应的值为该顶点的父节点
print("%d - %d wight:%d"%(parent[i]+1, i+1, cost[i][parent[i]]))
#统计最小生成树的总权值
minCost = minCost + cost[i][parent[i]];
print("总权值为:%d"%(minCost))
#根据用户提供了图的信息(存储在 cost 列表中),寻找最小生成树
def find_MST(cost):
#key 列表用于记录 B 类顶点到 A 类顶点的权值
#parent 列表用于记录最小生成树中各个顶点父节点的位置,便于最终生成最小生成树
#visited 列表用于记录各个顶点属于 A 类还是 B 类
parent = [-1]*V
key = [float('inf')]*V
visited = [False]*V
# 选择 key 列表中第一个顶点,开始寻找最小生成树
key[0] = 0
parent[0]= -1
# 对于 V 个顶点的图,最需选择 V-1 条路径,即可构成最小生成树
for x in range(V-1):
# 从 key 列表中找到权值最小的顶点所在的位置
u = min_Key(key,visited)
visited[u] = True
# 由于新顶点加入 A 类,因此需要更新 key 列表中的数据
for v in range(V):
# 如果类 B 中存在到下标为 u 的顶点的权值比 key 列表中记录的权值还小,表明新顶点的加入,使得类 B 到类 A 顶点的权值有了更好的选择
if cost[u][v] !=0 and visited[v] == False and cost[u][v] < key[v]:
# 更新 parent 列表记录的各个顶点父节点的信息
parent[v] = u
# 更新 key 列表
key[v] = cost[u][v]
# 根据 parent 记录的各个顶点父节点的信息,输出寻找到的最小生成树
print_MST(parent,cost);
find_MST(cost)
以图 1 为例,其中顶点 A、B、C、D、S、T 分别用 1~6 表示,以上程序的输出结果均为:
1 5 7
1 3 3
5 3 8
1 2 6
2 3 4
2 4 2
3 4 3
2 6 5
4 6 2
-1 -1
最小生成树为:
4 - 2 wight:2
1 - 3 wight:3
3 - 4 wight:3
1 - 5 wight:7
4 - 6 wight:2
总权值为:17

 媳妇等我以后给你一个家i
媳妇等我以后给你一个家i
